数据库系统---关系数据理论
问题的提出
表设计的好不好？
数据冗余+增删改异常
为什么有问题？
数据依赖关系 y=f(x)
eg：sname=f(sno)
eg：Student(Sno,Sdept,Mname,Cno,Grade)
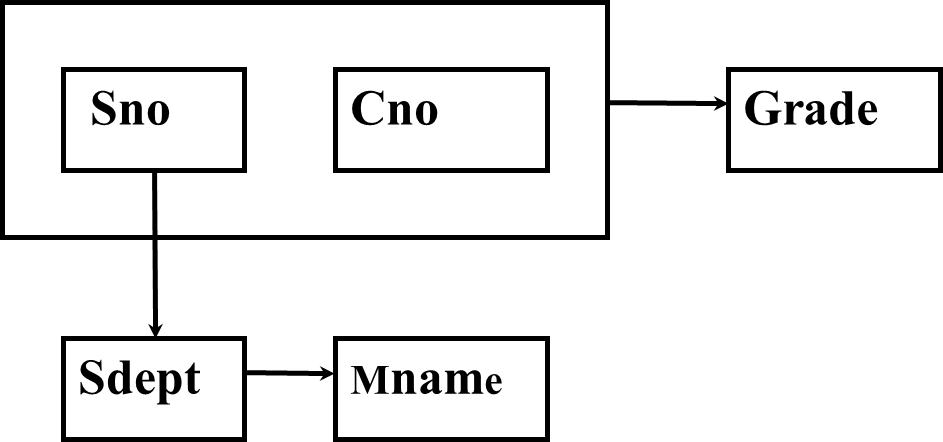
合适的函数依赖关系
(Sno,Cno)---Grade SC（Sno,Cno,Grade）
Grade与Sno,Cno有关
有不合适的函数依赖关系
(Sno,Cno)---Sdept---Mname
Sdept和Mname只与Sno有关
数据依赖关系有哪些？
（函数依赖 FD y=f(x) vs 多值依赖x=f(y) MVD（不合适））
函数依赖关系
（完全依赖 vs 部分依赖（不合适））
（传递依赖（不合适））
Sno->Sdept->Mname
（平凡依赖（不合适） vs 非平凡依赖）
范式理论
函数依赖
定义 设R(U)是一个属性集U上的关系模式，X和Y是U的子集。若对于R(U)的任意一个可能的关系r，r 中不可能存在两个元组在X上的属性值相等， 而在Y上的属性值不等， 则称“X函数确定Y”或“Y函数依赖于X”，记作X→Y。
eg：Student(Sno,Sdept,Mname,Cno,Grade)
假设不允许重名：
Sno → Ssex， Sno → Sage
Sno → Sdept， Sno ←→ Sname
Sname → Ssex， Sname → Sage
Sname → Sdept
平凡函数依赖与非平凡函数依赖
X→Y，但Y⊈X则称X→Y是非平凡的函数依赖。
X决定Y，Y与X一点关系也没有
X→Y，但Y⊆X 则称X→Y是平凡的函数依赖。
X决定Y，Y属于X
对于任一关系模式，平凡函数依赖都是必然成立的，它不反映新的语义。
若不特别声明， 我们总是讨论非平凡函数依赖。
完全函数依赖与部分函数依赖
定义 在R(U)中，如果X→Y，并且对于X的任何一个真子集X’, 都有 X’ ↛ Y, 则称Y对X完全函数依赖，记作X →F Y。
若X→Y，但Y不完全函数依赖于X，则称Y对X部分函数依赖，记作X →P Y
传递函数依赖
范式
范式是符合某一种级别的关系模式的集合。
关系数据库中的关系必须满足一定的要求。满足不同程度要求的为不同范式。
范式的种类：
各种范式之间存在联系：
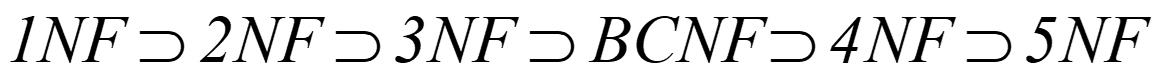
某一关系模式R为第n范式，可简记为R∈nNF。
一个低一级范式的关系模式，通过模式分解（schema decomposition）可以转换为若干个高一级范式的关系模式的集合，这种过程就叫规范化（normalization）。
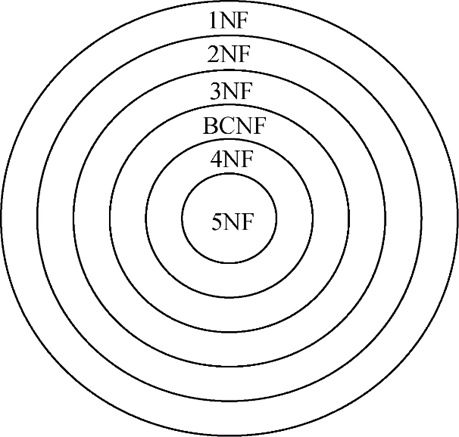
BCNF之后的4NF与5NF是多值依赖
1NF
定义：关系中每一分量不可再分。即不能以集合、序列等作为属性。（也就是不能表中套表，要保证数据的原子性。）
不满足1NF，因为{C1，C2，C3}和{C1，C4}是集合。
2NF
定义：每一个非主属性都完全函数依赖于任何一个候选码（消除非主属性对键的部分依赖）
eg：[例] S-L-C(Sno,Sdept,Sloc,Cno,Grade)， Sloc为学生的住处，并且每个系的学生住在同一个地方。S-L-C的码为(Sno,Cno)。
函数依赖有
(Sno,Cno)→（F）Grade
Sno→Sdept, (Sno,Cno)→（P）Sdept
Sno→Sloc, (Sno,Cno)→（P）Sloc
Sdept→Sloc
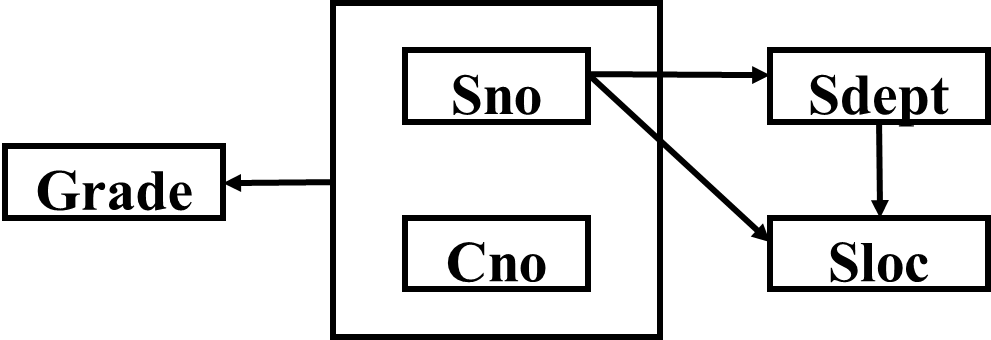
非主属性Sdept、Sloc并不完全依赖于码
关系模式S-L-C不属于2NF
消除非主属性对候选码的部份依赖
怎么进行模式分解？
S-L-C(Sno,Sdept,Sloc,Cno,Grade)：（拆表：谁对你好，复制自己，把它带走）
SC(Sno,Cno,Grade)
S-L(Sno,Sdept,Sloc)
当主码只有一个，不存在完整部分的关系
3NF
定义：消除非主属性对键的传递依赖
eg：
SC(Sno,Cno,Grade)
S-L(Sno,Sdept,Sloc)（拆表：谁对你好，复制自己，把它带走）
S-D(Sno,Sdept)∈ 3NF
D-L(Sdept,Sloc)∈ 3NF
BCNF
定义：消除主属性对码的部分和传递函数依赖
判断方式：
1.将所有的依赖关系列出来，如果左边都是候选码，则满足BCNF
2.主属性内部没有对码的部分和传递函数依赖
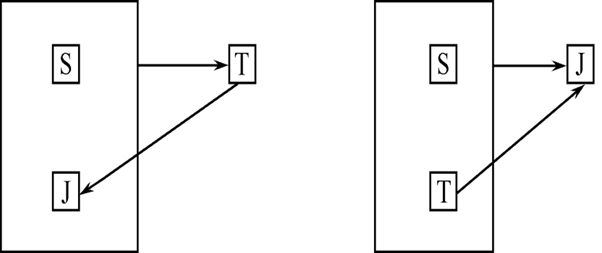
eg：[例6.8] 关系模式STJ(S,T,J)中，S表示学生，T表示教师，J表示课程。每一教师只教一门课。每门课有若干教师，某一学生选定某门课，就对应一个固定的教师。
由语义可得到函数依赖：(S,J)→T；(S,T)→J；T→J
因为没有任何非主属性对码传递依赖或部分依赖，STJ ∈ 3NF。
因为T是决定因素，而T不包含码，所以STJ ∈（/） BCNF关系。
